Парадокс времени ожидания, или почему мой автобус всегда опаздывает?
Если вы часто ездите на общественном транспорте, то наверняка встречались с такой ситуацией:
По идее, если автобусы приходят каждые 10 минут, а вы придёте в случайное время, то среднее ожидание должно составлять около 5 минут. Но в действительности автобусы не прибывают точно по расписанию, поэтому вы можете ждать дольше. Оказывается, при некоторых разумных предположениях можно прийти к поразительному выводу:
При ожидании автобуса, который приходит в среднем каждые 10 минут, ваше среднее время ожидания будет 10 минут.
Это то, что иногда называют парадоксом времени ожидания.
Идея встречалась мне раньше, и я всегда задавался вопросом, правда ли это на самом деле… насколько такие «разумные предположения» соответствуют действительности? В этой статье мы исследуем парадокс времени ожидания с точки зрения как моделирования, так и вероятностных аргументов, а затем взглянем на некоторые реальные данные автобусов в Сиэтле, чтобы (надеюсь) решить парадокс раз и навсегда.
Если автобусы прибывают ровно каждые десять минут, то действительно среднее время ожидания составит 5 минут. Можно легко понять, почему добавление вариаций в интервал между автобусами увеличивает среднее время ожидания.
Парадокс времени ожидания является частным случаем более общего явления — парадокса инспекции, который подробно обсуждается в толковой статье Аллена Дауни «Парадокс инспекции повсюду вокруг нас».
Короче говоря, парадокс инспекции возникает всякий раз, когда вероятность наблюдения количества связана с наблюдаемым количеством. Аллен приводит пример анкетирования студентов университета о среднем размере их классов. Хотя школа правдиво говорит о среднем количестве 30 студентов в группе, но средний размер группы с точки зрения студентов гораздо больше. Причина в том, что в больших классах (естественно) больше студентов, что и выявляется при их опросе.
В случае автобусного графика с заявленным 10-минутным интервалом иногда промежуток между прибытиями длиннее 10 минут, а иногда и короче. И если придти на остановку в случайное время, то у вас больше вероятность столкнуться с более длинным интервалом, чем с более коротким. И поэтому логично, что средний промежуток времени, между интервалами ожидания дольше, чем средний промежуток времени между автобусами, потому что более длинные интервалы чаще встречаются в выборке.
Но парадокс времени ожидания делает более сильное заявление: если средний интервал между автобусами составляет минут, то среднее время ожидания для пассажиров составляет минут. Может ли такое быть правдой?
Чтобы убедить себя в разумности этого, сначала смоделируем поток автобусов, которые прибывают в среднем за 10 минут. Для точности возьмём большую выборку: миллион автобусов (или примерно 19 лет круглосуточного 10-минутного трафика):
Проверим, что средний интервал близок к :
Теперь можем смоделировать прибытие большого количества пассажиров на автобусную остановку в течение этого промежутка времени и вычислить время ожидания, которое каждый из них испытывает. Инкапсулируем код в функцию для последующего использования:
Затем смоделируем время ожидания и вычислим среднее:
Среднее время ожидания близко к 10 минутам, как и предсказывал парадокс.
Как смоделировать такую ситуацию?
По сути, это пример парадокса инспекции, где вероятность наблюдения значения связана с самим значением. Обозначим через распределение интервалов между автобусами по мере их прибытия на остановку. В такой записи ожидаемое значение времени прибытия будет:
В предыдущей симуляции мы выбрали минут.
Когда пассажир прибывает на автобусную остановку в произвольное время, вероятность времени ожидания будет зависеть не только от , но и от самого : чем больше интервал, тем больше в нём пассажиров.
Таким образом, можно написать распределение времени прибытия с точки зрения пассажиров:
Константа пропорциональности выводится из нормализации распределения:
Это упрощается до
Тогда время ожидания будет составлять половину ожидаемого интервала для пассажиров, поэтому мы можем записать
что можно переписать более понятным образом:
и теперь остаётся только выбрать форму для и вычислить интегралы.
Получив формальную модель, каково же разумное распределение для ? Выведем картину распределения в пределах наших моделируемых прибытий, построив гистограмму интервалов между прибытиями:
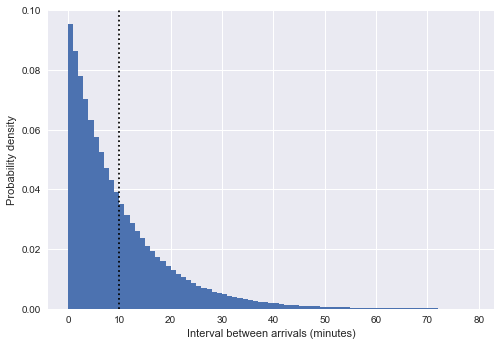
Здесь вертикальная пунктирная линия показывает средний интервал около 10 минут. Это очень похоже на экспоненциальное распределение, и не случайно: наше моделирование времени прибытия автобуса в виде однородных случайных чисел очень близко к процессу Пуассона, а для такого процесса распределение интервалов экспоненциально.
(Примечание: в нашем случае это только приблизительная экспонента; на самом деле интервалы между равномерно отобранными точками в пределах промежутка времени соответствуют бета-распределению , которое в большом пределе приближается к . Для более подробной информации можете почитать, например, пост на StackExchange или эту ветку в твиттере).
Экспоненциальное распределение интервалов подразумевает, что время прибытия следует за процессом Пуассона. Чтобы проверить это рассуждение, проверим наличие другого свойства пуассоновского процесса: что число прибытий в течение фиксированного промежутка времени является пуассоновским распределенем. Для этого разобъём симулированные прибытия на часовые блоки:
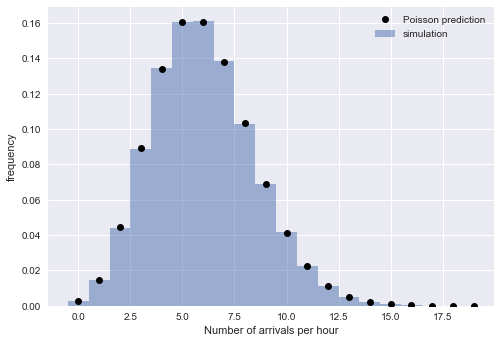
Близкое соответствие эмпирических и теоретических значений убеждает в правильности нашей интерпретации: для больших смоделированное время прибытия хорошо описано пуассоновским процессом, который подразумевает экспоненциально распределённые интервалы.
Это означает, что можно записать распределение вероятностей:
Если подставить результат в предыдущую формулу, то мы найдём среднее время ожидания для пассажиров на остановке:
Для рейсов с прибытиями по процессу Пуассона ожидаемое время ожидания идентично среднему интервалу между прибытиями.
Об этой проблеме можно рассуждать так: процесс Пуассона — это процесс без памяти, то есть история событий не имеет никакого отношения к ожидаемому времени следующего события. Поэтому по приходу на автобусную остановку среднее время ожидания автобуса всегда одинаково: в нашем случае это 10 минут, независимо от того, сколько времени прошло с момента предыдущего автобуса! При этом не имеет значения, как долго вы уже ждали: ожидаемое время до следующего автобуса всегда ровно 10 минут: в пуассоновском процессе вы не получаете «кредит» за время, проведённое в ожидании.
Вышеизложенное хорошо, если реальные прибытия автобусов на самом деле описываются процессом Пуассона, но так ли это?
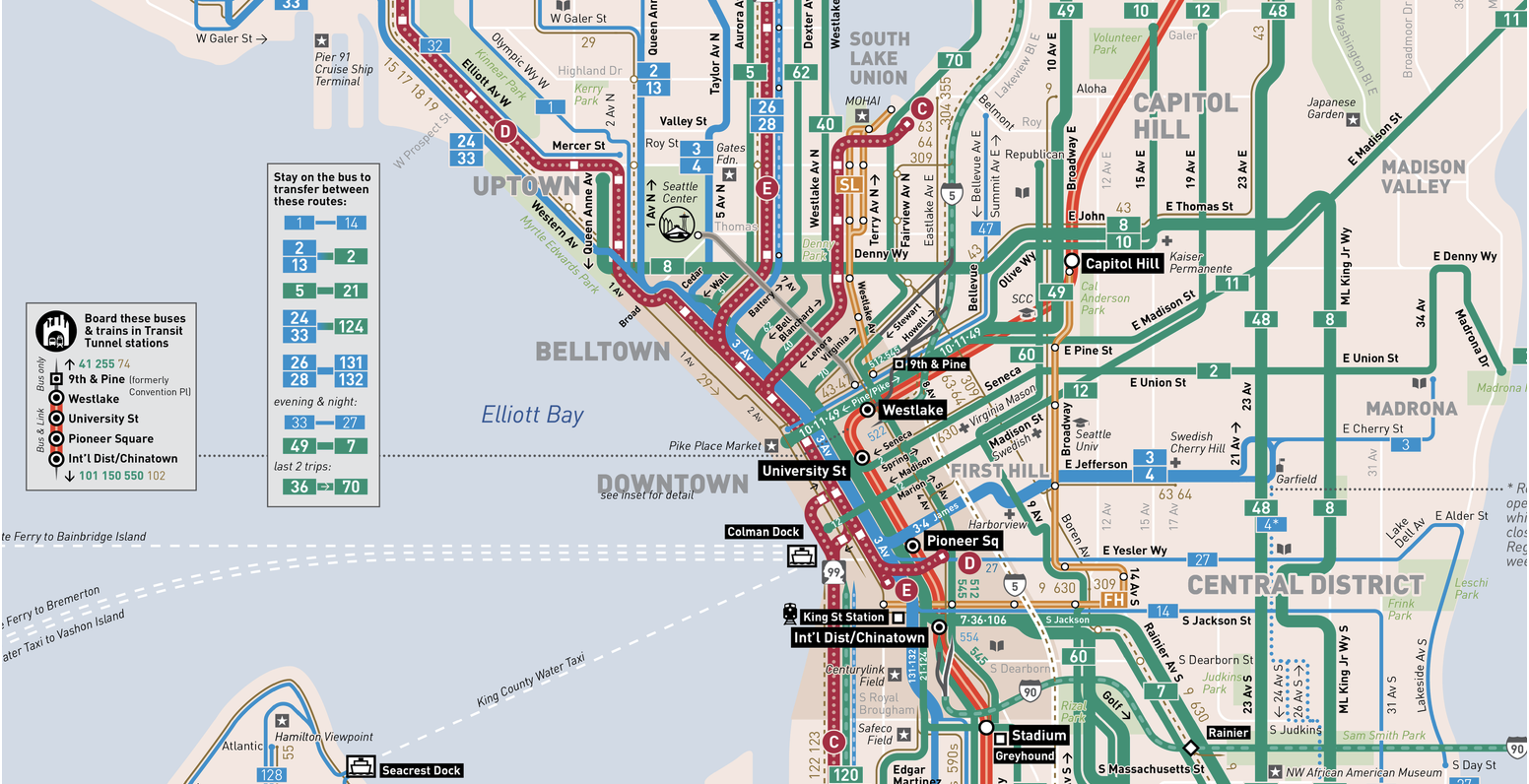
Источник: схема общественного транспорта Сиэтла
Попробуем определить, как парадокс времени ожидания согласуется с реальностью. Для этого изучим некоторые данные, доступные для загрузки здесь: arrival_times.csv (CSV-файл объёмом 3 МБ). Набор данных содержит запланированное и фактическое время прибытия для автобусов RapidRide маршрутов C, D и E на автобусной остановке 3rd&Pike в центре Сиэтла. Данные записаны во втором квартале 2016 года (огромное спасибо Марку Халленбеку из транспортного центра штата Вашингтон за этот файл!).
Я выбрал данные RapidRide в том числе потому что на протяжении большей части дня автобусы курсируют с регулярными интервалами 10−15 минут, не говоря уже о том, что я частый пассажир маршрута С.
Для начала сделаем небольшую очистку данных, чтобы преобразовать их в удобный вид:
В этой таблице шесть наборов данных: направления на север и юг для каждого маршрута C, D и E. Чтобы получить представление об их характеристиках, давайте построим гистограмму фактического минус запланированного времени прибытия для каждого из этих шести:

Логично предположить, что автобусы ближе к графику в начале маршрута и больше отклоняются от него к концу. Данные подтверждают это: наша остановка на южном маршруте С, а также на северных D и Е близка к началу маршрута, а в обратном направлении — недалеко от конечного пункта.
Посмотрим на наблюдаемые и запланированные интервалы между автобусами для этих шести маршрутов. Начнём с функции
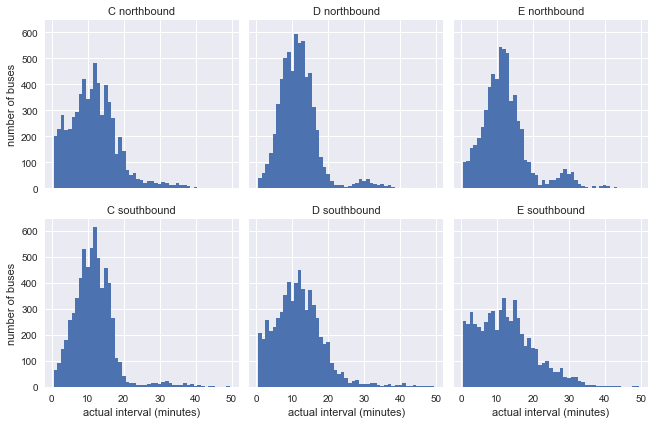
Уже видно, что результаты не очень похожи на экспоненциальное распределение нашей модели, но это ещё ничего не говорит: на распределения могут влиять непостоянные интервалы в графике.
Повторим построение диаграмм, взяв запланированные, а не наблюдаемые интервалы прибытия:
Это показывает, что в течение недели автобусы ходят с разными интервалами, так что мы не можем оценить точность парадокса времени ожидания по реальной информации с остановки.
Хотя официальный график не даёт однородных интервалов, есть несколько конкретных промежутков времени с большим количеством автобусов: например, почти 2000 автобусов маршрута E в северную сторону с запланированным интервалом в 10 минут. Чтобы узнать, применим ли парадокс времени ожидания, давайте сгруппируем данные по маршрутам, направлениям и запланированному интервалу, а затем повторно сложим их, словно они произошли последовательно. Это должно сохранить все соответствующие характеристики исходных данных, облегчив при этом прямое сравнение с предсказаниями парадокса времени ожидания.
На очищенных данных можно составить график распределения фактического появления автобусов по каждому маршруту и направлению с частотой прибытия:

Мы видим, что для каждого маршрута распределение наблюдаемых интервалов почти гауссово. Оно достигает максимума около запланированного интервала и имеет стандартное отклонение, которое меньше в начале маршрута (на юг для C, на север для D/E) и больше в конце. Даже на глаз видно, что фактические интервалы прибытия определённо не соответствуют экспоненциальному распределению, что является основным предположением, на котором основан парадокс времени ожидания.
Мы можем взять функцию моделирования времени ожидания, которую использовали выше, чтобы найти среднее время ожидания для каждого автобусного маршрута, направления и расписания:
Среднее время ожидания, возможно, на минуту или две больше половины запланированного интервала, но не равно запланированному интервалу, как подразумевает парадокс времени ожидания. Другими словами, парадокс инспекции подтверждён, но парадокс времени ожидания не соответствует действительности.
Парадокс времени ожидания был интересной отправной точкой для обсуждения, которое включило в себя моделирование, теорию вероятности и сравнение статистических предположений с реальностью. Хотя мы подтвердили, что в реальном мире автобусные маршруты подчиняются некоторой разновидности парадокса инспекции, приведённый выше анализ довольно убедительно показывает: основное предположение, лежащее в основе парадокса времени ожидания, — что прибытие автобусов следует статистике пуассоновского процесса — не является обоснованным.
Оглядываясь назад, это и не удивительно: процесс Пуассона — это процесс без памяти, который предполагает, что вероятность прибытия полностью независима от времени с момента предыдущего прибытия. На самом деле в хорошо управляемой системе общественного транспорта есть специально структурированные расписания, чтобы избежать такого поведения: автобусы не начинают свои маршруты в случайное время в течение дня, а стартуют по расписанию, выбранному для наиболее эффективной перевозки пассажиров.
Более важный урок в том, что следует быть осторожным относительно предположений, которые вы делаете к любой задаче анализа данных. Иногда процесс Пуассона — хорошие описание для данных о времени прибытия. Но только то, что один тип данных звучит как другой тип данных, не означает, что предположения, допустимые для одного, обязательно действительны для другого. Часто предположения, которые кажутся правильными, могут привести к выводам, которые не соответствуют действительности.
Вы приходите на остановку. Написано, что автобус ходит каждые 10 минут. Засекаете время… Наконец, через 11 минут приходит автобус и мысль: почему мне всегда не везёт?
По идее, если автобусы приходят каждые 10 минут, а вы придёте в случайное время, то среднее ожидание должно составлять около 5 минут. Но в действительности автобусы не прибывают точно по расписанию, поэтому вы можете ждать дольше. Оказывается, при некоторых разумных предположениях можно прийти к поразительному выводу:
При ожидании автобуса, который приходит в среднем каждые 10 минут, ваше среднее время ожидания будет 10 минут.
Это то, что иногда называют парадоксом времени ожидания.
Идея встречалась мне раньше, и я всегда задавался вопросом, правда ли это на самом деле… насколько такие «разумные предположения» соответствуют действительности? В этой статье мы исследуем парадокс времени ожидания с точки зрения как моделирования, так и вероятностных аргументов, а затем взглянем на некоторые реальные данные автобусов в Сиэтле, чтобы (надеюсь) решить парадокс раз и навсегда.
Парадокс инспекции
Если автобусы прибывают ровно каждые десять минут, то действительно среднее время ожидания составит 5 минут. Можно легко понять, почему добавление вариаций в интервал между автобусами увеличивает среднее время ожидания.
Парадокс времени ожидания является частным случаем более общего явления — парадокса инспекции, который подробно обсуждается в толковой статье Аллена Дауни «Парадокс инспекции повсюду вокруг нас».
Короче говоря, парадокс инспекции возникает всякий раз, когда вероятность наблюдения количества связана с наблюдаемым количеством. Аллен приводит пример анкетирования студентов университета о среднем размере их классов. Хотя школа правдиво говорит о среднем количестве 30 студентов в группе, но средний размер группы с точки зрения студентов гораздо больше. Причина в том, что в больших классах (естественно) больше студентов, что и выявляется при их опросе.
В случае автобусного графика с заявленным 10-минутным интервалом иногда промежуток между прибытиями длиннее 10 минут, а иногда и короче. И если придти на остановку в случайное время, то у вас больше вероятность столкнуться с более длинным интервалом, чем с более коротким. И поэтому логично, что средний промежуток времени, между интервалами ожидания дольше, чем средний промежуток времени между автобусами, потому что более длинные интервалы чаще встречаются в выборке.
Но парадокс времени ожидания делает более сильное заявление: если средний интервал между автобусами составляет минут, то среднее время ожидания для пассажиров составляет минут. Может ли такое быть правдой?
Имитация времени ожидания
Чтобы убедить себя в разумности этого, сначала смоделируем поток автобусов, которые прибывают в среднем за 10 минут. Для точности возьмём большую выборку: миллион автобусов (или примерно 19 лет круглосуточного 10-минутного трафика):
import numpy as np
N = 1000000 # number of buses
tau = 10 # average minutes between arrivals
rand = np.random.RandomState(42) # universal random seed
bus_arrival_times = N * tau * np.sort(rand.rand(N))Проверим, что средний интервал близок к :
intervals = np.diff(bus_arrival_times)
intervals.mean()9.9999879601518398 Теперь можем смоделировать прибытие большого количества пассажиров на автобусную остановку в течение этого промежутка времени и вычислить время ожидания, которое каждый из них испытывает. Инкапсулируем код в функцию для последующего использования:
def simulate_wait_times(arrival_times,
rseed=8675309, # Jenny's random seed
n_passengers=1000000):
rand = np.random.RandomState(rseed)
arrival_times = np.asarray(arrival_times)
passenger_times = arrival_times.max() * rand.rand(n_passengers)
# find the index of the next bus for each simulated passenger
i = np.searchsorted(arrival_times, passenger_times, side='right')
return arrival_times[i] - passenger_timesЗатем смоделируем время ожидания и вычислим среднее:
wait_times = simulate_wait_times(bus_arrival_times)
wait_times.mean()10.001584206227317 Среднее время ожидания близко к 10 минутам, как и предсказывал парадокс.
Копаем глубже: вероятности и пуассоновские процессы
Как смоделировать такую ситуацию?
По сути, это пример парадокса инспекции, где вероятность наблюдения значения связана с самим значением. Обозначим через распределение интервалов между автобусами по мере их прибытия на остановку. В такой записи ожидаемое значение времени прибытия будет:
В предыдущей симуляции мы выбрали минут.
Когда пассажир прибывает на автобусную остановку в произвольное время, вероятность времени ожидания будет зависеть не только от , но и от самого : чем больше интервал, тем больше в нём пассажиров.
Таким образом, можно написать распределение времени прибытия с точки зрения пассажиров:
Константа пропорциональности выводится из нормализации распределения:
Это упрощается до
Тогда время ожидания будет составлять половину ожидаемого интервала для пассажиров, поэтому мы можем записать
что можно переписать более понятным образом:
и теперь остаётся только выбрать форму для и вычислить интегралы.
Выбор p(T)
Получив формальную модель, каково же разумное распределение для ? Выведем картину распределения в пределах наших моделируемых прибытий, построив гистограмму интервалов между прибытиями:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.hist(intervals, bins=np.arange(80), density=True)
plt.axvline(intervals.mean(), color='black', linestyle='dotted')
plt.xlabel('Interval between arrivals (minutes)')
plt.ylabel('Probability density');
Здесь вертикальная пунктирная линия показывает средний интервал около 10 минут. Это очень похоже на экспоненциальное распределение, и не случайно: наше моделирование времени прибытия автобуса в виде однородных случайных чисел очень близко к процессу Пуассона, а для такого процесса распределение интервалов экспоненциально.
(Примечание: в нашем случае это только приблизительная экспонента; на самом деле интервалы между равномерно отобранными точками в пределах промежутка времени соответствуют бета-распределению , которое в большом пределе приближается к . Для более подробной информации можете почитать, например, пост на StackExchange или эту ветку в твиттере).
Экспоненциальное распределение интервалов подразумевает, что время прибытия следует за процессом Пуассона. Чтобы проверить это рассуждение, проверим наличие другого свойства пуассоновского процесса: что число прибытий в течение фиксированного промежутка времени является пуассоновским распределенем. Для этого разобъём симулированные прибытия на часовые блоки:
from scipy.stats import poisson
# count the number of arrivals in 1-hour bins
binsize = 60
binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int))
x = np.arange(20)
# plot the results
plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation')
plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction')
plt.xlabel('Number of arrivals per hour')
plt.ylabel('frequency')
plt.legend();
Близкое соответствие эмпирических и теоретических значений убеждает в правильности нашей интерпретации: для больших смоделированное время прибытия хорошо описано пуассоновским процессом, который подразумевает экспоненциально распределённые интервалы.
Это означает, что можно записать распределение вероятностей:
Если подставить результат в предыдущую формулу, то мы найдём среднее время ожидания для пассажиров на остановке:
Для рейсов с прибытиями по процессу Пуассона ожидаемое время ожидания идентично среднему интервалу между прибытиями.
Об этой проблеме можно рассуждать так: процесс Пуассона — это процесс без памяти, то есть история событий не имеет никакого отношения к ожидаемому времени следующего события. Поэтому по приходу на автобусную остановку среднее время ожидания автобуса всегда одинаково: в нашем случае это 10 минут, независимо от того, сколько времени прошло с момента предыдущего автобуса! При этом не имеет значения, как долго вы уже ждали: ожидаемое время до следующего автобуса всегда ровно 10 минут: в пуассоновском процессе вы не получаете «кредит» за время, проведённое в ожидании.
Время ожидания в реальности
Вышеизложенное хорошо, если реальные прибытия автобусов на самом деле описываются процессом Пуассона, но так ли это?

Источник: схема общественного транспорта Сиэтла
Попробуем определить, как парадокс времени ожидания согласуется с реальностью. Для этого изучим некоторые данные, доступные для загрузки здесь: arrival_times.csv (CSV-файл объёмом 3 МБ). Набор данных содержит запланированное и фактическое время прибытия для автобусов RapidRide маршрутов C, D и E на автобусной остановке 3rd&Pike в центре Сиэтла. Данные записаны во втором квартале 2016 года (огромное спасибо Марку Халленбеку из транспортного центра штата Вашингтон за этот файл!).
import pandas as pd
df = pd.read_csv('arrival_times.csv')
df = df.dropna(axis=0, how='any')
df.head()| OPD_DATE | VEHICLE_ID | RTE | DIR | TRIP_ID | STOP_ID | STOP_NAME | SCH_STOP_TM | ACT_STOP_TM | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2016-03-26 | 6201 | 673 | S | 30908177 | 431 | 3RD AVE & PIKE ST (431) | 01:11:57 | 01:13:19 |
| 1 | 2016-03-26 | 6201 | 673 | S | 30908033 | 431 | 3RD AVE & PIKE ST (431) | 23:19:57 | 23:16:13 |
| 2 | 2016-03-26 | 6201 | 673 | S | 30908028 | 431 | 3RD AVE & PIKE ST (431) | 21:19:57 | 21:18:46 |
| 3 | 2016-03-26 | 6201 | 673 | S | 30908019 | 431 | 3RD AVE & PIKE ST (431) | 19:04:57 | 19:01:49 |
| 4 | 2016-03-26 | 6201 | 673 | S | 30908252 | 431 | 3RD AVE & PIKE ST (431) | 16:42:57 | 16:42:39 |
Я выбрал данные RapidRide в том числе потому что на протяжении большей части дня автобусы курсируют с регулярными интервалами 10−15 минут, не говоря уже о том, что я частый пассажир маршрута С.
Очистка данных
Для начала сделаем небольшую очистку данных, чтобы преобразовать их в удобный вид:
# combine date and time into a single timestamp
df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM'])
df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM'])
# if scheduled & actual span midnight, then the actual day needs to be adjusted
minute = np.timedelta64(1, 'm')
hour = 60 * minute
diff_hrs = (df['actual'] - df['scheduled']) / hour
df.loc[diff_hrs > 20, 'actual'] -= 24 * hour
df.loc[diff_hrs < -20, 'actual'] += 24 * hour
df['minutes_late'] = (df['actual'] - df['scheduled']) / minute
# map internal route codes to external route letters
df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category')
df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category')
# extract useful columns
df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy()
df.head()| Маршрут | Направление | График | Факт. прибытие | Опоздание (мин) | |
|---|---|---|---|---|---|
| 0 | C | юг | 2016-03-26 01:11:57 | 2016-03-26 01:13:19 | 1.366667 |
| 1 | C | юг | 2016-03-26 23:19:57 | 2016-03-26 23:16:13 | -3.733333 |
| 2 | C | юг | 2016-03-26 21:19:57 | 2016-03-26 21:18:46 | -1.183333 |
| 3 | C | юг | 2016-03-26 19:04:57 | 2016-03-26 19:01:49 | -3.133333 |
| 4 | C | юг | 2016-03-26 16:42:57 | 2016-03-26 16:42:39 | -0.300000 |
На сколько опаздывают автобусы?
В этой таблице шесть наборов данных: направления на север и юг для каждого маршрута C, D и E. Чтобы получить представление об их характеристиках, давайте построим гистограмму фактического минус запланированного времени прибытия для каждого из этих шести:
import seaborn as sns
g = sns.FacetGrid(df, row="direction", col="route")
g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20))
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('minutes late', 'number of buses');
Логично предположить, что автобусы ближе к графику в начале маршрута и больше отклоняются от него к концу. Данные подтверждают это: наша остановка на южном маршруте С, а также на северных D и Е близка к началу маршрута, а в обратном направлении — недалеко от конечного пункта.
Запланированные и наблюдаемые интервалы
Посмотрим на наблюдаемые и запланированные интервалы между автобусами для этих шести маршрутов. Начнём с функции
groupby в Pandas для вычисления этих интервалов:def compute_headway(scheduled):
minute = np.timedelta64(1, 'm')
return scheduled.sort_values().diff() / minute
grouped = df.groupby(['route', 'direction'])
df['actual_interval'] = grouped['actual'].transform(compute_headway)
df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway)g = sns.FacetGrid(df.dropna(), row="direction", col="route")
g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5)
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('actual interval (minutes)', 'number of buses');
Уже видно, что результаты не очень похожи на экспоненциальное распределение нашей модели, но это ещё ничего не говорит: на распределения могут влиять непостоянные интервалы в графике.
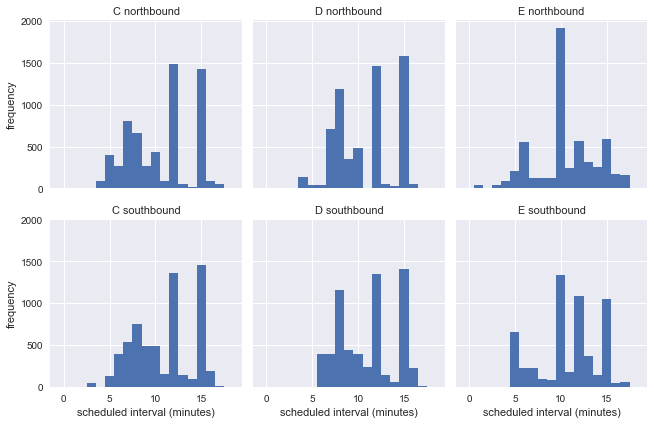
Повторим построение диаграмм, взяв запланированные, а не наблюдаемые интервалы прибытия:
g = sns.FacetGrid(df.dropna(), row="direction", col="route")
g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5)
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('scheduled interval (minutes)', 'frequency');
Это показывает, что в течение недели автобусы ходят с разными интервалами, так что мы не можем оценить точность парадокса времени ожидания по реальной информации с остановки.
Построение однородных расписаний
Хотя официальный график не даёт однородных интервалов, есть несколько конкретных промежутков времени с большим количеством автобусов: например, почти 2000 автобусов маршрута E в северную сторону с запланированным интервалом в 10 минут. Чтобы узнать, применим ли парадокс времени ожидания, давайте сгруппируем данные по маршрутам, направлениям и запланированному интервалу, а затем повторно сложим их, словно они произошли последовательно. Это должно сохранить все соответствующие характеристики исходных данных, облегчив при этом прямое сравнение с предсказаниями парадокса времени ожидания.
def stack_sequence(data):
# first, sort by scheduled time
data = data.sort_values('scheduled')
# re-stack data & recompute relevant quantities
data['scheduled'] = data['scheduled_interval'].cumsum()
data['actual'] = data['scheduled'] + data['minutes_late']
data['actual_interval'] = data['actual'].sort_values().diff()
return data
subset = df[df.scheduled_interval.isin([10, 12, 15])]
grouped = subset.groupby(['route', 'direction', 'scheduled_interval'])
sequenced = grouped.apply(stack_sequence).reset_index(drop=True)
sequenced.head()| Маршрут | Направление | Расписание | Факт. прибытие | Опоздание (мин) | Факт. интервал | Интервал по графику | |
|---|---|---|---|---|---|---|---|
| 0 | C | север | 10.0 | 12.400000 | 2.400000 | NaN | 10.0 |
| 1 | C | север | 20.0 | 27.150000 | 7.150000 | 0.183333 | 10.0 |
| 2 | C | север | 30.0 | 26.966667 | -3.033333 | 14.566667 | 10.0 |
| 3 | C | север | 40.0 | 35.516667 | -4.483333 | 8.366667 | 10.0 |
| 4 | C | север | 50.0 | 53.583333 | 3.583333 | 18.066667 | 10.0 |
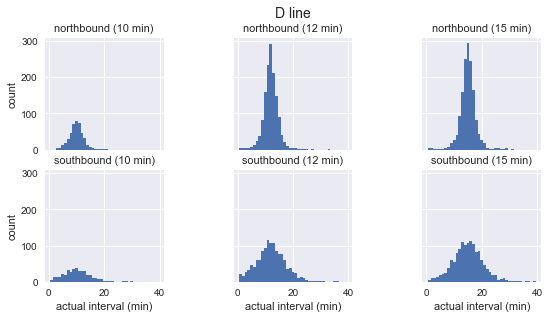
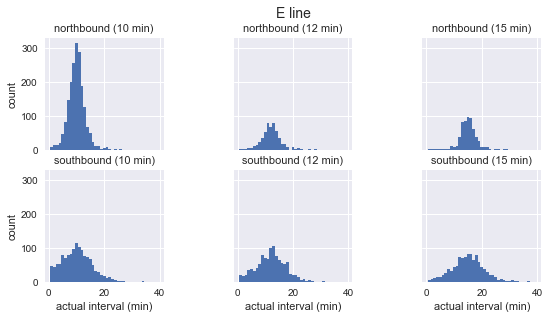
На очищенных данных можно составить график распределения фактического появления автобусов по каждому маршруту и направлению с частотой прибытия:
for route in ['C', 'D', 'E']:
g = sns.FacetGrid(sequenced.query(f"route == '{route}'"),
row="direction", col="scheduled_interval")
g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5)
g.set_titles('{row_name} ({col_name:.0f} min)')
g.set_axis_labels('actual interval (min)', 'count')
g.fig.set_size_inches(8, 4)
g.fig.suptitle(f'{route} line', y=1.05, fontsize=14)


Мы видим, что для каждого маршрута распределение наблюдаемых интервалов почти гауссово. Оно достигает максимума около запланированного интервала и имеет стандартное отклонение, которое меньше в начале маршрута (на юг для C, на север для D/E) и больше в конце. Даже на глаз видно, что фактические интервалы прибытия определённо не соответствуют экспоненциальному распределению, что является основным предположением, на котором основан парадокс времени ожидания.
Мы можем взять функцию моделирования времени ожидания, которую использовали выше, чтобы найти среднее время ожидания для каждого автобусного маршрута, направления и расписания:
grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval'])
sims = grouped['actual'].apply(simulate_wait_times)
sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std()))маршрут направление интервал по расписанию
C север 10.0 7.8 +/- 12.5
12.0 7.4 +/- 5.7
15.0 8.8 +/- 6.4
юг 10.0 6.2 +/- 6.3
12.0 6.8 +/- 5.2
15.0 8.4 +/- 7.3
D север 10.0 6.1 +/- 7.1
12.0 6.5 +/- 4.6
15.0 7.9 +/- 5.3
юг 10.0 6.7 +/- 5.3
12.0 7.5 +/- 5.9
15.0 8.8 +/- 6.5
E север 10.0 5.5 +/- 3.7
12.0 6.5 +/- 4.3
15.0 7.9 +/- 4.9
юг 10.0 6.8 +/- 5.6
12.0 7.3 +/- 5.2
15.0 8.7 +/- 6.0
Name: actual, dtype: objectСреднее время ожидания, возможно, на минуту или две больше половины запланированного интервала, но не равно запланированному интервалу, как подразумевает парадокс времени ожидания. Другими словами, парадокс инспекции подтверждён, но парадокс времени ожидания не соответствует действительности.
Заключение
Парадокс времени ожидания был интересной отправной точкой для обсуждения, которое включило в себя моделирование, теорию вероятности и сравнение статистических предположений с реальностью. Хотя мы подтвердили, что в реальном мире автобусные маршруты подчиняются некоторой разновидности парадокса инспекции, приведённый выше анализ довольно убедительно показывает: основное предположение, лежащее в основе парадокса времени ожидания, — что прибытие автобусов следует статистике пуассоновского процесса — не является обоснованным.
Оглядываясь назад, это и не удивительно: процесс Пуассона — это процесс без памяти, который предполагает, что вероятность прибытия полностью независима от времени с момента предыдущего прибытия. На самом деле в хорошо управляемой системе общественного транспорта есть специально структурированные расписания, чтобы избежать такого поведения: автобусы не начинают свои маршруты в случайное время в течение дня, а стартуют по расписанию, выбранному для наиболее эффективной перевозки пассажиров.
Более важный урок в том, что следует быть осторожным относительно предположений, которые вы делаете к любой задаче анализа данных. Иногда процесс Пуассона — хорошие описание для данных о времени прибытия. Но только то, что один тип данных звучит как другой тип данных, не означает, что предположения, допустимые для одного, обязательно действительны для другого. Часто предположения, которые кажутся правильными, могут привести к выводам, которые не соответствуют действительности.
- 32673 reads
Who's online
There are currently 1 user and 9 guests online.


